Propiedades de funciones exponenciales y logarítmicas.
Las características generales de las funciones exponenciales son:
1) El dominio de una función exponencial es R.
2) Su recorrido es (0, +∞) .
3) Son funciones continuas.
4) Como a0 = 1 , la función siempre pasa por el punto (0, 1).
La función corta el eje Y en el punto (0, 1) y no corta el eje X.
5) Como a1 = a , la función siempre pasa por el punto (1, a).
6) Si a > 1 la función es creciente.
Si 0 < a < 1 la función es decreciente.
7) Son siempre concavas.
8) El eje X es una asíntota horizontal.
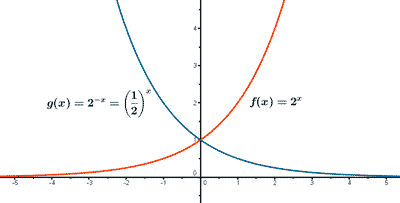
Ejemplo de funciones exponenciales: f(x) = 2x g(x) = 2 - x = (1/2)x
Las características generales de las funciones logarítmicas son:
1) El dominio de una función logarítmica son los números reales positivos: Dom(f) = (0. + ∞) .
2) Su recorrido es R: Im(f) = R .
3) Son funciones continuas.
4) Como loga1 = 0 , la función siempre pasa por el punto (1, 0) .
La función corta el eje X en el punto (1, 0) y no corta el eje Y.
5) Como logaa = 1 , la función siempre pasa por el punto (a, 1) .
6) Si a > 1 la función es creciente.
Si 0 < a < 1 la función es decreciente.
7) Son convexas si a > 1 .
Son concavas si 0 < a < 1 .
8) El eje Y es una asíntota vertical.
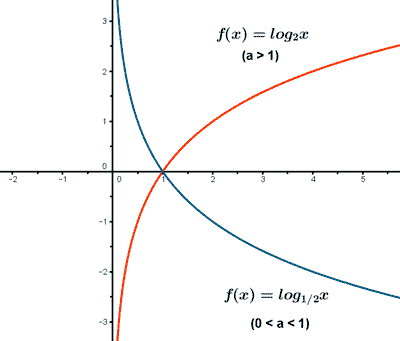
Ejemplo de funciones logarítmicas: f(x) = log2x
g(x) = log1/2x